Eric Naud (AFM)
Vous vous en êtes sans doute déjà aperçu, tout n'est pas aussi idyllique que le premier chapitre pourrait le laisser supposer, et dans la pratique, le système cristallin ne saute pas toujours aux yeux. Les principales complications tiennent à deux raisons : d'abord les cristaux présentent la plupart du temps des faces autres que celles de la maille primitive ; ensuite, au sein d'un même système cristallin, ces nouvelles faces, que dans un premier temps et par abus de langage nous appellerons « troncatures », seront différentes selon le niveau de symétrie de la maille. Revenez, on va détailler ça tranquillement.
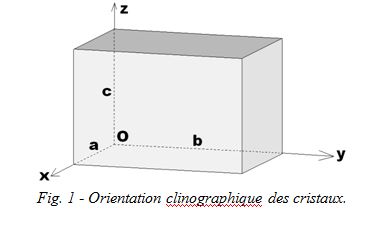
Deux petites précisions, cependant, avant les détails : d'abord, tous les dessins de cristaux qui vont suivre (à l'exception de quelques-uns clairement signalés), sont en orientation dite « clinographique », maintenant communément admise au niveau international. Par convention, cela signifie que la longueur a, située sur l'axe Ox est celle venant vers vous légèrement sur la gauche ; la longueur b, sur l'axe Oy, part à droite un peu en avant du plan du papier, et la longueur c, sur l'axe Oz est verticale, dans le plan du papier. Le point O et les trois axes Ox, Oy et Oz nous serviront plus tard pour indexer les faces des cristaux. Pour l'instant, on met ça de côté.
Deuxièmement, est-il besoin de vous le dire, les belles couleurs que j'ai utilisées dans certains de mes schémas ne sont là que pour vous aider à repérer les faces identiques.
1) Troncatures
Donc, comme quel que soit le système cristallin, les cristaux présentent très souvent des faces autres que celles définies par leur maille primitive. En conséquence, leur aspect extérieur est la plupart du temps bien plus complexe que celui des modèles que vous avez découpés tout à l'heure.
Une fois de plus, je vais utiliser un exemple qui est dans tous les bouquins, mais il est tellement clair qu'on va s'en servir encore un coup. Voyons donc comment par « troncature » on passe du cube à l'octaèdre.
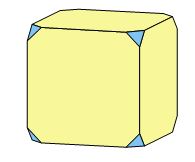
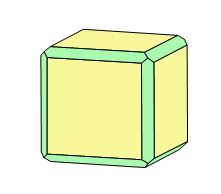
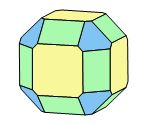
Prenez un beau cube de galène, et imaginez que d'un coup de votre burin le plus affûté, vous fassiez sauter de manière égale les huit sommets : vous obtenez un cube tronqué par huit faces identiques, inclinées à 45° par rapport aux faces du cube (fig. 2).
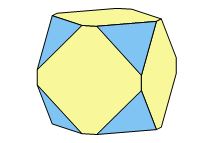
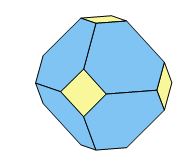
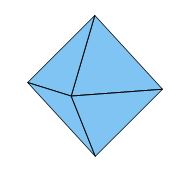
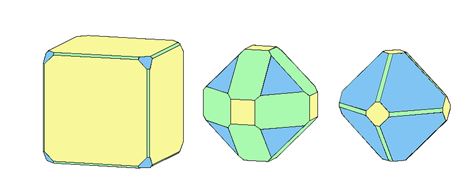
Ces nouvelles faces peuvent être à peine visibles, ou au contraire très importantes (fig. 3). A l'extrême, elles peuvent même faire disparaître totalement les six faces d'origine pour ne plus laisser subsister qu'un solide à huit faces, l'octaèdre (fig. 4).
Fig. 2 - Cube modifié par les faces de l'octaèdre
Fig. 3 – Variations de proportion entre les faces du cube et de l'octaèdre.
Fig. 4 - Octaèdre.
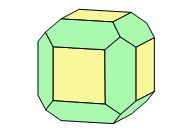
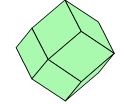
Répétons la même opération en tronquant non plus les sommets, mais les douze arêtes (fig. 5). Si nous rapprochons progressivement les nouvelles faces du centre du cristal, nous obtenons un nouveau solide à douze faces, le dodécaèdre rhomboïdal (fig. 6).
Fig. 5 - Cube modifié par le dodécaèdre.
Fig.6 - Evolution du cube en dodécaèdre.
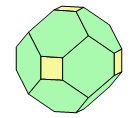
On peut également tronquer à la fois les huit sommets et les douze arêtes du cube
(fig. 7).
Fig. 7 - Cube modifié par l'octaèdre et le dodécaèdre.
Evidemment, les faces du cube, de l'octaèdre et du dodécaèdre, peuvent se combiner dans des proportions très variables. Si vous connaissez bien la galène, les cristaux de la figure 8 ne vous surprendront pas.
Fig. 8 - Différentes proportions entre les faces du cube, de l'octaèdre et du dodécaèdre.
Le plus important est de bien comprendre les deux points suivants. Premièrement, notez que pour faire apparaître l'octaèdre, nous avons simplement remplacé huit éléments du cube (les sommets) par huit faces. De même pour le dodécaèdre, dont les douze faces ont remplacé les douze arêtes du cube. Dans les deux cas, nous avons totalement respecté la symétrie de départ du cube (on va voir ça de plus près dans cinq minutes).
Deuxièmement, et ceci quelles que soient les proportions respectives des faces, les angles qu'elles forment entre elles ne changent pas. C'est la fameuse loi de constance des angles établie par Romé de l'Isle il y a plus de deux cent ans. Ceci est vrai pour absolument tous les minéraux et tous les systèmes cristallins. Pour le même minéral, l'angle entre deux faces données ne peut par exemple en aucun cas être de 68° sur un cristal, et de 72° sur un autre. Si c'est le cas, c'est qu'il ne s'agit pas des mêmes faces, ou bien ce n'est pas le même minéral.
Le dodécaèdre et l'octaèdre sont donc bien des formes rattachées au système cubique, même si au premier abord elles semblent n'avoir que peu de points communs avec le cube.
ATTENTION : si j'ai parlé de faire sauter des morceaux du cristal de départ, c'était uniquement pour vous aider à visualiser la disposition des nouvelles faces. En fait, dans la nature, c'est le contraire qui se produit : si un cristal est octaédrique et non pas cubique, ce n'est pas parce que le Génie des Géodes est venu écorner les sommets du cube, mais parce que les sommets octaédriques ont poussé plus vite. Idem pour les sommets dodécaédriques.
Explication du phénomène :
Fig. 9 - Germe initial en forme de cube.
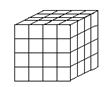
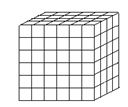
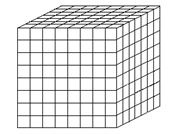
Au départ, il se forme un germe de cristal composé de molécules cubiques alignées (fig. 9). Si la matière cristallise lentement et dans un milieu peu agité, les molécules se déposent en couches régulières, et le cristal grossit en conservant sa forme (fig. 10) :
Fig. 10 - Croissance d'un cube.
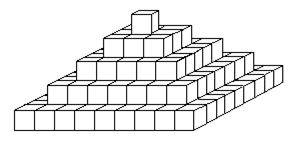
Dans certains cas, comme par exemple une cristallisation rapide, les niveaux ne seront pas complets. Chacun sera en retrait par rapport au niveau inférieur, chaque face du cube de départ prenant alors petit à petit un aspect de pyramide de Chéops.
J'avais essayé de vous faire un dessin, mais vu le résultat, vous allez devoir vous débrouiller par vous-même. Achetez des apéricubes (le paquet géant), et avant l'apéritif, entraînez-vous à construire d'abord un cube, de la taille que vous voulez. Vous devriez y arriver sans trop de problèmes, et en tirer une première conclusion : avec plein de petits cubes, on peut en faire un plus grand.
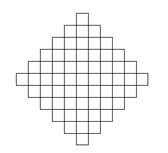
Prenez ensuite un miroir, posez-le à plat, et dressez dessus une pyramide, en plaçant la base selon le dessin ci-dessous :
Fig. 11 - Modèle pour l'octaèdre.
Montez les rangs en retrait de un apéricube à chaque fois : vous verrez, ô merveille, un octaèdre prendre forme sur votre miroir. Avant de les manger, dessinez avec vos petits bouts de fromage un carré de 9 de côté (représentant une face d'un cube), et dressez sur celle-ci une pyramide régulière.
Fig. 12 - Construction d'un sommet du dodécaèdre.
Revenez au dessin du dodécaèdre (fig. 6). Si vous êtes observateur, vous constaterez que votre pyramide correspond à un des sommets de cette figure, chacun des quatre pans de la pyramide pouvant être assimilé à une demi face de cristal. Imaginez que vous faites la même chose sur les six faces d'un cube : vous venez de reconstituer tout seul un dodécaèdre.
Vous me direz que ces faces ne sont pas planes, qu'elles sont une succession d'arêtes et de creux : c'est vrai, mais c'est à l'échelle atomique. A l'échelle de la vision humaine, et même sous un microscope électronique, il n'apparaît qu'une face plane. Cela explique cependant pourquoi certaines faces cristallines sont plus brillantes que d'autres, ou striées selon une direction précise.
Si vous n'aimez pas les apéricubes, ou si vous les boycottez en soutien à Jean-Pierre Coffe, prenez un tabouret à surface carrée, et laissez couler du sable dessus, jusqu'à ce que plus un grain ne tienne : vous venez de simuler, d'une manière sans doute peu académique, mais très explicite, la croissance des faces de la pyramide précédente sur une face du cube.
Nous venons de montrer, avec finalement pas grand-chose, que l'on pouvait reconstituer l'octaèdre et le dodécaèdre à partir de briques cubiques. La cristallographie vous semble t-elle plus claire, tout à coup ?
ATTENTION : de tout le chapitre précédent, on peut déduire que ce que nous appelions au début par commodité les faces « principales », ne sont pas plus principales que les faces octaédriques ou dodécaédriques. Toutes ne sont que des formes créées par un empilement de molécules. On ne va pas trop s'étendre là-dessus, mais ce doit être clair dans les esprits : un cristal n'est jamais tronqué au sens littéral du terme, il y a simplement certaines parties qui se sont développées plus ou moins vite, en fonction de des caractères de la maille cristalline, et de l'environnement physicochimique.
Pourquoi telle face plutôt qu'une autre ? Ce n'est plus dans nos compétences d'amateurs. Les amorces d'explications que je vous ai fournies quelques lignes plus haut ne sont que des exemples, et ce domaine est encore mal connu.
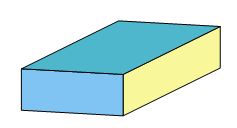
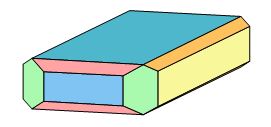
Voici maintenant un cristal de baryte montrant uniquement les formes simples du système orthorhombique, ce qui pour ce minéral n'est pas l'habitus le plus fréquent, mais il faut toujours compter avec la chance...
Fig. 13 – Cristal « simple » de baryte.
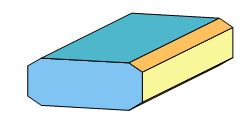
Dans ce système, les trois dimensions ne sont pas toutes équivalentes. Une même troncature n'affectera pas tous les éléments de la maille primitive, mais seulement ceux identiques. Ainsi une troncature sur les arêtes ne pourra toucher que celles de même orientation (fig. 14), car comme pour le système cubique, il est impératif de respecter la symétrie de départ du cristal orthorhombique (un peu de patience, j'ai dit).
Fig. 14 - Baryte.
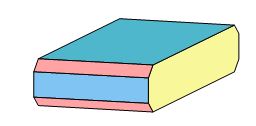
Il existe deux autres possibilités, suivant des arêtes différentes (fig. 15) :
Fig. 15 – Baryte.
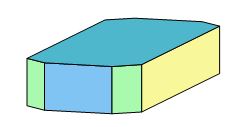
Les douze arêtes du cristal simple peuvent bien sûr être tronquées (fig. 16) :
Fig. 16 - Baryte.
Mais dans le système orthorhombique, les trois dimensions de la maille cristalline sont différentes, et par suite, les angles que les troncatures formeront avec les faces de la maille primitive ne seront pas tous égaux.
Ceci mérite une explication : quand nous avons empilé des briques cubiques en marquant un rang de retrait, la face octaédrique ainsi obtenue formait un angle de 45° avec les faces du cube (revoyez les figures 2 à 8, ainsi que 11 à 12). Si l'on fait la même chose avec des briques orthorhombiques, la nouvelle face est plus inclinée par rapport à l'un des côtés de la maille (fig. 17).
Fig. 17 - Inclinaison d'une troncature par rapport aux faces de la maille orthorhombique.
Ainsi dans le cas de la baryte (fig. 16), les faces roses recoupent les bleu-clair à 58°11 et les bleu-vert à 31°49 ; les faces vertes recoupent les jaunes à 39°10 et les bleu-clair à 50°50 ; les faces orangées recoupent les bleu-vert à 37°18, et les jaunes à 52°42. Plus généralement, avec un peu d'expérience, et même sans goniomètre, la reconnaissance des faces cristallines et des angles associés est un bon moyen pour les amateurs d'identifier certains minéraux (distinction anglésite / baryte, par exemple).
Confronté à un cristal n'étant pas exactement semblable à l'une des mailles primitives décrites dans le chapitre précédent, il faudra donc d'abord essayer de retrouver quelles faces sont venues la modifier. Dans un deuxième temps, c'est l'observation de ces troncatures qui permettra éventuellement l'identification du minéral.
Mais bien sûr, si c'était si simple, ce serait facile (et réciproquement). De tout ce qui précède, vous avez sans doute déjà compris que les troncatures n'affectent pas les cristaux au petit bonheur. Non seulement leur inclinaison par rapport aux faces correspondant à la maille primitive n'est en aucun cas le fruit du hasard, mais pour tel minéral, certaines se répètent en plus ou moins grand nombre, alors qu'elles sont presque totalement absentes chez tel autre appartenant pourtant au même système cristallin, ou bien elles présentent un aspect très différent.
En fait, comme je l'ai brièvement évoqué un peu plus haut, les troncatures se développent en fonction du niveau de symétrie de la maille cristalline. Je me doute bien que ça ne vous fait pas plaisir, mais on n'est pas là pour rigoler.