Eric Naud (AFM)
D'accord, mon titre est un peu provocateur, mais vous l'avez bien cherché. Combien de fois ai-je entendu lors de nos petites réunions :
« Oui mais moi, en cristallo, je suis nul ! »
Allons donc ! Et tant qu'on y est, la cristallographie serait pour le commun des mortels une tare génétique, et un don inné chez quelques veinards ? Désolé pour ceux que l'idée d'utiliser cet alibi aurait effleurés, mais la cristallo, c'est une chose qui s'apprend. Au début on n'y pige rien, c'est hermétique au possible, ça colle la ²migraine, mais ça s'apprend. De toute façon, un minimum de connaissances en cette matière est indispensable au minéralogiste amateur s'il veut se prétendre tel, et se différencier du simple collectionneur de minéraux, fussent-ils micros.
Cependant il faut bien admettre, à la décharge des soi-disant « nuls », que les manuels à l’usage des amateurs rendent souvent l'approche de la cristallographie particulièrement rébarbative : indices de Miller, pinacoïde, notation de Schöenflies-Fédorov, hémiédrie énantiomorphe, stéréogramme,... il y a de quoi se décourager, surtout si l'on ne possède pas quelques bases en mathématiques.
Pour contourner le problème et rendre la cristallographie plus accessible, je vais tenter de faire la synthèse de ce qui est réellement utile à l'amateur, en attaquant le sujet sous un angle différent et en éliminant ce qui s'adresse plutôt aux professionnels, ou tout au moins aux amateurs dits "chevronnés". Ultérieurement, vous pourrez aborder à votre rythme les notions plus complexes, qui passeront d'autant mieux que vous aurez bien assimilé ce qui va suivre.Car en fait, nous n'avons pas réellement besoin de grand chose, nous autres minéralogistes de terrain : la plupart du temps, reconnaître simplement le système cristallin de nos échantillons suffirait à notre bonheur.Mais pour reconnaître, il faut connaître. La première chose absolument indispensable est donc de se mettre en tête les principales caractéristiques des sept systèmes cristallins. Ca demande un petit effort, mais c'est beaucoup plus facile que vous ne croyez.
I) Caractéristiques sommaires des sept systèmes cristallins
D'abord, un petit rappel de chimie : tout cristal est un empilement régulier de « briques » appelées molécules, elles-mêmes constituées d'atomes (voir articles sur la chimie, parus dans ce même cahier il y a quelques années). Un système cristallin est défini par la forme de sa maille primitive, c'est-à-dire la forme des « briques » qui vont constituer le cristal.
Pour se représenter ces briques, on n'a pas encore trouvé mieux que le cristal de calcite. Cet exemple est dans tous les bouquins, mais il est toujours préférable de « sentir » le phénomène, de l'expérimenter soi-même. Faites donc l'essai chez vous sur un vieux cristal ébréché, vous verrez que ça marche à tous les coups : brisez-le autant de fois que vous voudrez, vous obtiendrez toujours des morceaux ayant la même forme « losangique » que la maille primitive, même en observant les plus petits débris à la bino.
Votre cristal était donc, avant que vous ne tapiez dessus comme un forcené, un empilement de briques de même forme, toutes orientées dans le même sens. Bien que ce soit particulièrement évident pour la calcite du fait de son excellent clivage, ceci est valable pour tous les minéraux.
Dans les cristaux, cette maille primitive peut avoir sept formes différentes, qu'il vous faut absolument mémoriser. Ceci n'est pas une figure de style, c'est vraiment une condition sine qua non pour aller plus loin : les caractéristiques de ces sept formes doivent être aussi imprimées en vous que l'alphabet, les tables de multiplication, votre numéro de sécu, ou le code confidentiel de votre carte bancaire.
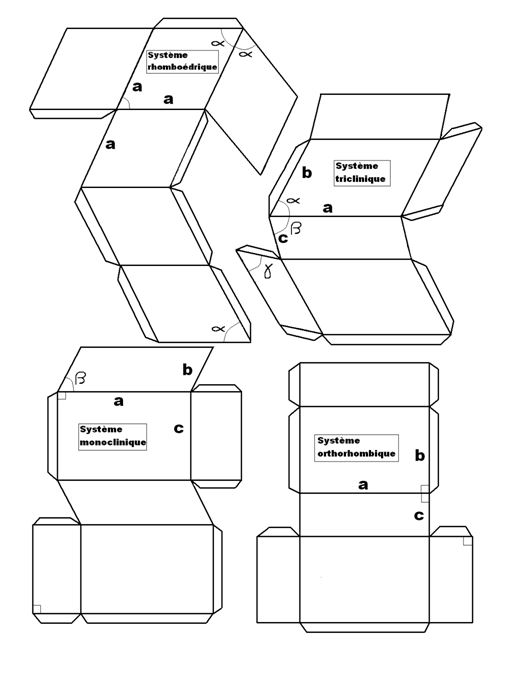
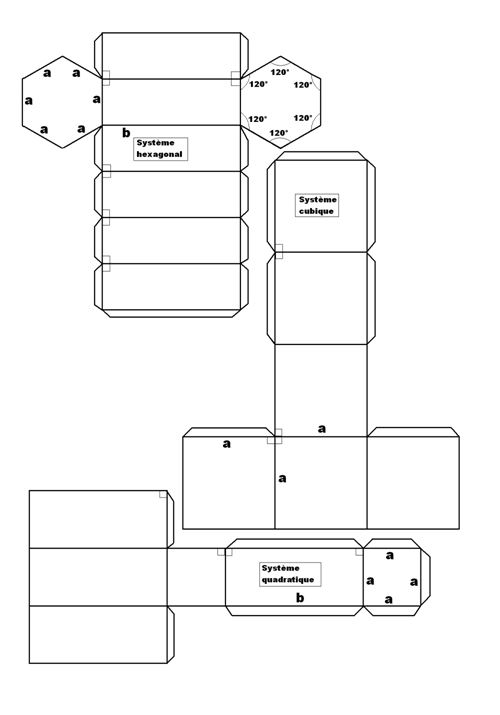
Pour vous faciliter la vie, vous trouverez ci-après deux planches de découpages, qui vous permettront de reconstituer les sept formes de base.
Je vous conseille de les télécharger, et de les éditer sur un papier fort de type bristol. Découpez, collez, puis reprenez la lecture.
*Planche n°1 à télécharger
*Planche n°2 à télécharger
Voilà. Vous devez maintenant avoir entre les mains sept magnifiques collages. Examinons-les en détail.
Premier point : vous constaterez qu'à l'exception du système hexagonal, les six autres sont des parallélépipèdes. Rappel de géométrie : un parallélépipède est un solide à six faces parallèles et égales deux à deux. Cela signifie que les faces parallèles sont identiques (mêmes angles et mêmes longueurs des côtés), et que toutes les arêtes parallèles sont de même longueur.
On remarque également que parmi ces six modèles, trois ne comportent que des angles droits, tandis que deux n'en comportent aucun. Deux ont leurs six faces identiques (cubique et rhomboédrique).
Laissez toujours de côté le système hexagonal. Prenez une des six figures restantes (celle que vous voulez). De chacun de ses sommets partent trois arêtes orientées selon trois directions différentes, et qui se recoupent selon trois angles. Pour l'instant, ces six valeurs (trois angles et trois longueurs) vont nous suffire pour définir la maille cristalline. Dans le chapitre qui va suivre, et par convention internationale, les trois arêtes (longueur, largeur, et hauteur) seront notées a, b et c, tandis que les trois angles qu'elles font entre elles seront nommés α, β, et γ. Voyons en détail ce que cela donne pour chaque modèle.
I-1) Système cubique :
On commence facile. N'importe quel élève de fin de maternelle sait qu'un cube est un solide dont les trois dimensions sont égales, et forment entre elles des angles droits. Les caractéristiques de la maille seront donc résumées par les deux formules suivantes :
a = b = c
α = β = γ = 90°0
Quelques exemples connus : fluorite, pyrite, halite.
I-2) Système quadratique :
Ce système est également appelé tétragonal, notamment dans les publications étrangères (abrégé en tet. dans le Fleischer, par exemple).La maille primitive est un prisme droit (vertical, si vous préférez) à base carrée : deux dimensions sont égales, la troisième est différente (plus courte ou plus longue que les deux autres), et elles se recoupent toutes à angle droit.
Nous pouvons donc écrire :
a = b ≠ c
α = β = γ = 90°
- : le symbole ≠ signifie « non égal à »).
Comparaisons possibles : une boîte micro 28x28x22, une règle de bureau à section carrée, un carreau de faïence 15x15.
Quelques exemples : autunite, zircon, apophyllite.
I-3) Système orthorhombique :
(synonyme en certaines langues : rhombic, ou rhombisch).
La maille orthorhombique primitive est un « pavé » : les trois dimensions se recoupent là encore à angle droit, mais elles sont toutes différentes. Ce sera donc un prisme droit à base rectangulaire, que nous pouvons résumer ainsi :
a ≠ b ≠ c
α = β = γ = 90°
Comparaisons possibles : un immeuble, un pack de lait, une brique...
Quelques exemples parlants : célestite, atacamite, baryte.
I-4) Système monoclinique :
Ca va toujours ? Parce que ça va se compliquer un peu.
Dans le système monoclinique, la maille est un prisme oblique à base rectangulaire, ou, vu sous un autre angle, un prisme vertical à base de parallélogramme (relisez, prenez votre temps, observez le collage correspondant). Les trois dimensions sont différentes, et forment entre elles deux angles droits et un angle quelconque.
a ≠ b ≠ c
α = γ = 90° ; ß ≠ 90°
Comparaisons possibles : un ciseau à bois taillé aux deux extrémités, une gomme, ou le toit d'une Citroën Ami 6, pour ceux qui ont connu.
Exemples typiques : gypse, érythrite, laumontite.
I-5) Système triclinique :
Encore plus raide : la maille primitive est un prisme oblique à base de parallélogramme : les trois dimensions sont différentes, de même que les trois angles. Il ne subsiste plus d'angle droit. Pour ceux qui l'auraient oublié (il n'y a pas de honte), rappelons qu'un parallélogramme est une figure plane à quatre côtés égaux et parallèles deux à deux. Chaque face de votre modèle triclinique en est un.
Les caractéristiques du modèle triclinique sont donc :
a ≠ b ≠ c
α ≠ β ≠ γ ≠ 90°
Comparaison possible : je n'ai rien trouvé, faites travailler votre imagination.
Minéraux nettement tricliniques : axinite, iimorite, laueite.
I-6) Système rhomboédrique :
Ce système est également nommé trigonal, y compris, et de plus en plus souvent, dans des ouvrages en langue française (abrégé en trig. dans le Fleischer).
Il ressemble à première vue au système triclinique, mais la maille est un prisme oblique à base losangique (parallélogramme dont les quatre côtés sont égaux), dans laquelle les trois dimensions et les trois angles sont égaux.
a = b = c
α = β = γ ≠ 90°
Minéraux rhomboédriques courants : calcite, jarosite, hématite.
I-7) Système hexagonal :
Un facile (en apparence) pour la fin. Même si ce n'est pas tout à fait vrai, nous considérerons pour votre tranquillité d'esprit que la maille est un prisme vertical à base hexagonale (rappel : un hexagone est une figure à six côtés égaux, faisant entre eux des angles de 120°).
Mais le prisme hexagonal n'est pas un parallélépipède. Pour le définir, nous allons utiliser deux de ses directions se coupant à 120°, et sa hauteur. Nous noterons donc :
a = b ≠ c
α = β = 90° ; γ = 120°
Exemples bien connus : apatite, béryl, néphéline.